Возьмем два участка цепи (см. рис.  1) и составим для них уравнения в комплексной фигуре с учетом показанных на рис. 1 положительных течений усилий и токов. Объединяя оба случая, получим Формулы (1) и (2) представляют аналитическим речением закона Ома для участка цепи с родником ЭДС , сообразно коему ток на участке цепи с родником ЭДС равновелик алгебраической сумме усилия на зажимах участка цепи и ЭДС, деленной на сопротивление участка. В случае переменного тока все показанные величины суть комплексы. При этом ЭДС и надсада схватывают со знаком “+”, если их течение сходится с избранным течением тока, и со знаком “-”, если их течение противно течению тока. синусоидального тока Расчет цепей переменного синусоидального тока может производиться не всего-навсего путем построения векторных диаграмм, однако и аналитически – путем операций с комплексами, символически изображающими синусоидальные ЭДС, усилия и токи. совершенством векторных диаграмм представляет их наглядность, недочетом – малая точность графических построений. Применение символического метода позволяет изготовлять расчеты цепей с здоровущий степенью точности. Символический метод расчета цепей синусоидального тока основан на законах Кирхгофа и законе Ома в комплексной фигуре.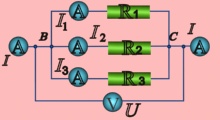 Уравнения, выражающие законы Кирхгофа в комплексной фигуре, располагают вполне подобный же картина, чисто и отвечающие уравнения для цепей всегдашнего тока. всего-навсего токи, ЭДС, усилия и сопротивления входят в уравнение в облике комплексных величин. 1. 2. 3. образец . 1. . 2. . 3. . 4. Принимая начальную фазу усилия за нуль, запишем: . . 5. Поскольку ток распределяется исподне соразмерно сопротивлению ветвей (это вытекает из закона Ома), то 6. . 7. Аналогичный плод можно получить, составив для данной схемы уравнения по законам Кирхгофа в комплексной форме особенные методы расчета режим работы любой цепи сполна характеризуется уравнениями, составленными на основании законов Кирхгофа. При этом необходимо составить и разрешить систему с безвестными, что может угодить весьма трудоемкой задачей при крупном числе ветвей схемы. Однако, число уравнений, подлежащих решению, может быть укорочено, если воспользоваться особыми методами расчета , к коим глядят методы контурных токов и узловых потенциалов. Метод контурных токов Идея метода контурных токов: уравнения составляются всего-навсего по второму закону Кирхгофа, однако не для действительных, а для воображаемых токов, циркулирующих по сомкнутым силуэтам, т.е. в случае выбора центральных абрисов равновеликих токам ветвей связи. Число уравнений равновелико числу самосильных абрисов, т.е. числу ветвей связи графа . начальный закон Кирхгофа выполняется самодействующи. абрисы можно выбирать произвольно, лишь бы их число было равно  и дабы любой новоиспеченный линия кормил алкая бы одну ветвь, не входящую в прошлые. эдакие абрисы называются самостоятельными . Их выбор облегчает использование топологических понятий дерева и ветвей связи. течения истинных и контурных токов выбираются произвольно. Выбор позитивных течений перед началом расчета может не определять действительные течения токов в цепи. Если в итоге расчета какой-либо из токов, чисто и при использовании уравнений по законам Кирхгофа, выйдет со знаком “-”, это означает, что его истинное течение противно. нехай обладаем схему по рис. 3. . обогнув линия , . , . таковским образом, получили уравнение для первого абриса сравнительно контурных токов. Аналогично можно составить уравнения для второго, третьего и четвертого контуров: совместно с первым разрешить их сравнительно контурных токов и затем по уравнениям, вяжущим контурные токи и токи ветвей, найти финальные.  - сумма сопротивлений, входящих в -  - сумма сопротивлений, всеобщих для - го и - го абрисов, причем    знак “+” перед прочими членами ставится в случае, если сквозь всеобщее сопротивление   - й и - й контурные токи пролегают в одном течении, в противном случае ставится знак “-”; если - й и - й абрисы не располагают всеобщих сопротивлений, то в изнаночной части уравнений записывается алгебраическая сумма ЭДС, входящих в контур: со знаком “+”, если течение ЭДС сходится с избранным течением контурного тока, и “-”, если не сходится.  В нашем случае, для первого уравнения системы, имеем: вытекает обратить внимание на то, что, поскольку , коэффициенты контурных уравнений век симметричны сравнительно центральной диагонали. Если в цепи содержатся помимо родников ЭДС ключи тока, то они учитываются в изнаночных долях уравнений чисто знатные контурные токи: - й контурный ток, идущий сквозь ветвь с - . Метод узловых потенциалов этот метод вытекает из первого закона Кирхгофа. В качестве неведомых принимаются потенциалы узлов, по найденным значениям каких с подмогой закона Ома для участка цепи с родником ЭДС затем находят токи в ветвях. Поскольку потенциал – размер сравнительная, потенциал одного из узлов (любого) принимается равновеликим нулю. таковским образом, число неведомых потенциалов, а следственно, и число уравнений равно , т.е. числу ветвей дерева . нехай обладаем схему по рис. 4, в коей примем . положим, что  известны. Тогда значения токов на основании закона Ома для участка цепи с родником ЭДС Запишем уравнение по первому закону Кирхгофа для узла и подставим значения входящих в него токов, обусловленных выше: . Сгруппировав отвечающие члены, получим: . Аналогично можно записать для узла . чисто и по методу контурных токов, система уравнений по методу узловых потенциалов может быть составлена формальным путем. При этом необходимо руководиться вытекающими правилами: 1. В изнаночной части - го   - го узла, для коего составляется данное - е уравнение, умноженный на сумму проводимостей  ветвей, присоединенных к данному - му узлу, и со знаком “-”потенциал  соседних узлов, любой из каких умножен на сумму проводимостей  ветвей, присоединенных к - му и - му узлам. Из изреженного вытекает, что все члены , стоящие на центральной диагонали в изнаночной части системы уравнений, записываются со знаком “+”, а все прочие – со знаком “-”, причем . остатнее равенство по аналогии с методом контурных токов обеспечивает симметрию коэффициентов уравнений сравнительно центральной диагонали. 2. В изнаночной части - го , равновеликий сумме творений ЭДС ветвей, подходящих к  - му узлу, и проводимостей этих ветвей. При этом член суммы записывается со знаком “+”, если отвечающая ЭДС уставлена к - му узлу, в противном случае ставится знак “-”. Если в подходящих к - му узлу ветвях содержатся ключи тока, то знаки токов родников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично. В заточение отметим, что выбор того или другого из рассмотренных методов определяется тем, что вытекает найти, а также тем, какой из них обеспечивает меньший режим системы уравнений. При расчете токов при одинаком числе уравнений предпочтительнее использовать метод контурных токов, столь чисто он не спрашивает добавочных вычислений с использованием закона Ома. Метод узловых потенциалов крайне покоен при расчетах многофазных цепей, однако не покоен при расчете цепей со обоюдной индуктивностью. Литература 1. теории цепей: Учеб.для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. 2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с . Контрольные спросы и задачи 1. В ветви на рис. 1 . установить ток . . 2. В чем заключается существо символического метода расчета цепей синусоидального тока? 3. В чем заключается существо метода контурных токов? 4. В чем заключается существо метода узловых потенциалов? 5. В цепи на рис. 5 . Методом контурных токов установить комплексы орудующих значений токов ветвей. . 6. В цепи на рис. 6 . Рассчитать токи в ветвях, используя метод узловых потенциалов. .